20th Century Analytical Techniques
All graduate music students are expected to demonstrate a competency with the basics of Set Theory and 12-tone theory. We use the text Introduction to Post-tonal Music by Josef Straus.
Set Theory - Sample Questions
Normal Order
Give the set of pitch classes in the example below in Normal Order.

Solution Click to expand
The Normal Order of this PC set is (10 1 2 3)
Give the set of pitch classes in the example below in Normal Order.
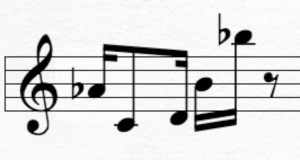
Solution Click to expand
The Normal Order of this PC set is (8 10 11 0 2)
Prime Form
Give the Prime Form of the set of pitch classes in the example below.

Solution Click to expand
The Prime Form for this PC set is (0 1 5 7)
Give the Prime Form of the set of pitch classes in the example below.

Solution Click to expand
The Prime Form for this PC set is (0 1 3 4 6 8)
Interval Vectors
Give the interval vector for the set of pitch classes in the example below.
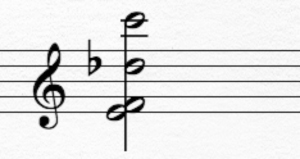
Solution Click to expand
The Interval Vector for this PC set is (2 0 1 2 1 0)
Give the interval vector for the set of pitch classes in the example below.
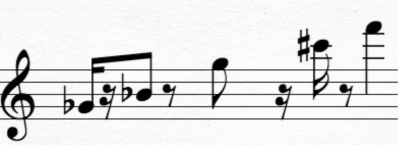
Solution Click to expand
The Interval Vector for this PC set is (2 1 2 2 2 1)
Symmetry in Unordered Sets
Which of the following sets is transpositionally symmetrical?
- A. (2 4 5 8)
- B. (6 9 0 2)
- C. ( 3 4 9 10)
- D. (1 3 6 8 11)
Solution Click to expand
Only set C. (3 4 9 10) is transpositionally symmetrical.
Which of the following sets are inversionally symmetrical but not transpositionally symmetrical?
- A. (2 4 5 8)
- B. (6 9 0 2)
- C. ( 3 4 9 10)
- D. (1 3 6 8 11)
Solution Click to expand
Set D. (1 3 6 8 11) is inversionally symmetrical but NOT transpositionally symmetrical. NOTE: Set C. (3 4 9 10) is both inversionally and transpositionally symmetrical.
12-tone Theory - Sample Questions
Use the 12-tone Matrix below to answer the rest of the questions.
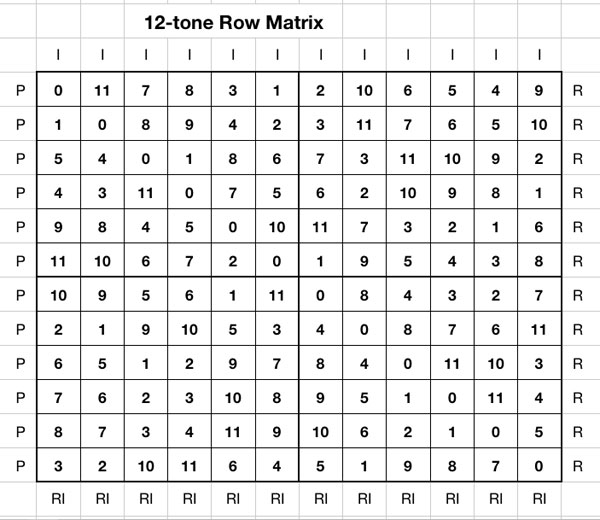
Basic Row Forms
Name the row that starts with the pitch classes 4 3 11...
Solution Click to expand
The row beginning with the pitch classes 4 3 11... is P4 (the prime row starting on 4)
Name the row that starts with the pitch classes 8 1 0...
Solution Click to expand
The row beginning with the pitch classes 8 1 0... is RI5 (the retrograde inversion row ending on 5)
Name the row form that starts with the pitch classes 4 5 9...
Solution Click to expand
The row beginning with the pitch classes 4 5 9... is I4 (the inversion row starting on 4)
Name the row form that starts with the pitch classes 4 11 0...
Solution Click to expand
The row beginning with the pitch classes 4 11 0... is R7 (retrograde row ending on 7)
Which row other than R2 can be used combinatorially with the row P2 (2 1 9 10 5 3 4 0 8 7 6 11)?
Solution Click to expand
The row I7 (7 8 0 4 11 6 5 9 1 2 3 10)
Find a row in the matrix that has two invariant trichords with the row R1 (10 5 6 7 11 3 2 4 9 8 0 1).
One Solution Click to expand
The row R1 (10 5 6 7 11 3 2 4 9 8 0 1) shares two invariant trichords with three different rows...I6 [(6 7 11) and (8 0 1)], I10 [(11 3 2) and (9 8 0)], and RI1 [(4 9 8) and (10 5 6)
In the example below determine the two row forms used (use the matrix above to help you out). Then do a '12-count' to show how the rows are used in the music.

Solution Click to expand
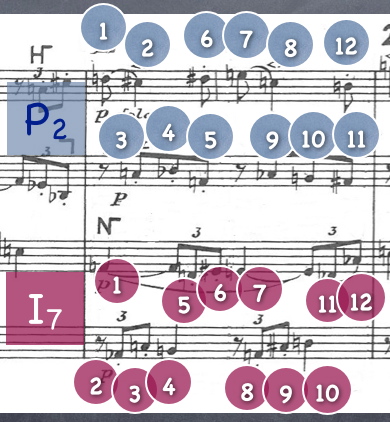 /div>
/div>